2025-02-19[DP]数字三角形模型

[动态规划]数字三角形模型

1. 动态规划分析方式—闫氏思考法

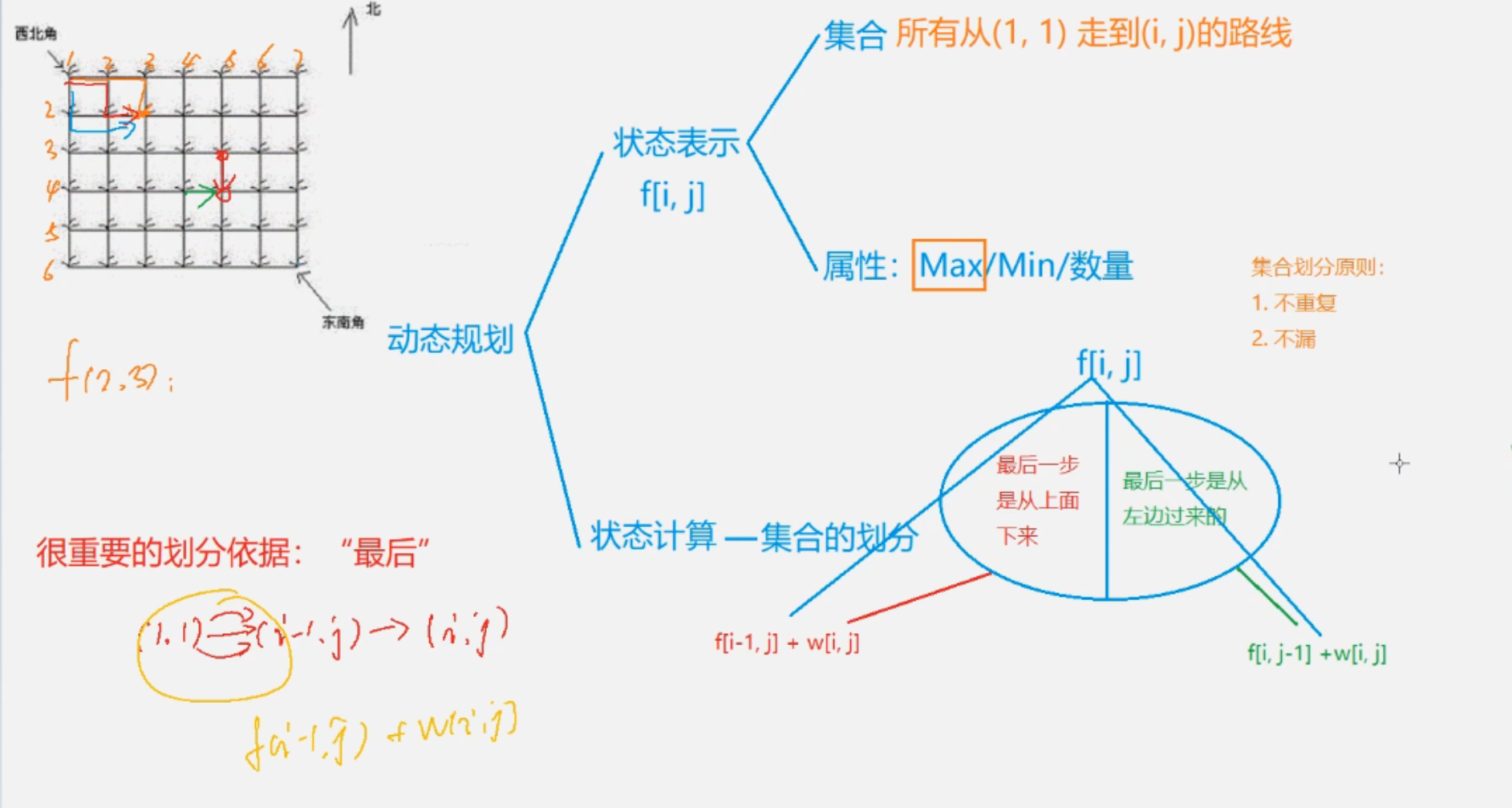
• 首先要设计一个状态表示的方法，体现在dp数组的设计，要求能够表示从开始到目标过程中所有用到的状态。
• 考虑状态的转移，实际上就是集合的划分，判断有几种情况能一步转移到当前的状态，集合划分的标准：不重复，不遗漏，这里有个技巧，一般看能一步到到最后一步的状态划分。

2. 数字三角型模型

• 网格，从左上到右下，只能单向走（不能回头），求累积的最大值/最小值

3. 注意事项

• 一般下标从1开始，因为涉及“i-1”操作，方便初始化。
• 当求最大值时，0行和0列就初始化成0，可以不动。
• 当求最小值时，就要具体分析，也可以直接做特判，不用0行和0列。

4.例题

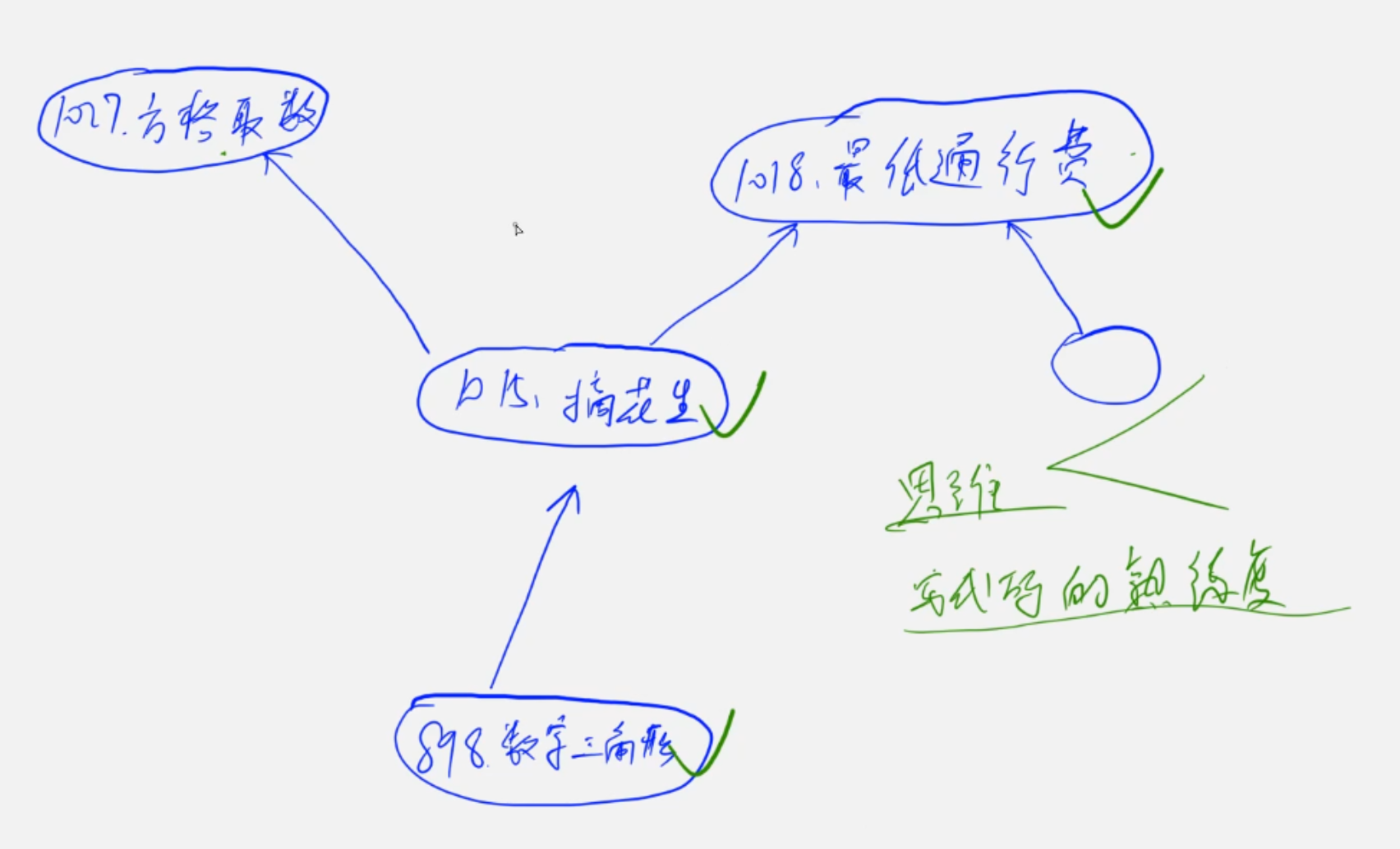
4.1 数字三角形

// https://www.luogu.com.cn/problem/P1216

#include<bits/stdc++.h>
using namespace std;

const int N=1010;

int a[N][N];
int dp[N][N];

void work(){
    int n;
    cin>>n;

    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++){
            cin>>a[i][j];
            dp[i][j]=max(dp[i-1][j-1]+a[i][j], dp[i-1][j]+a[i][j]);
        }

    int res=0;
    for(int i=1;i<=n;i++) res=max(res, dp[n][i]);

    cout<<res<<endl;    

}
        

int main(){
    work();
    return 0;
}

4.2 摘花生

// https://www.acwing.com/file_system/file/content/whole/index/content/4183962/

#include<bits/stdc++.h>
using namespace std;

const int N = 110;

int a[N][N];
int dp[N][N];

int n, m;

int t;

void work(){
    cin >> t;

    while(t--){
        cin >> n >> m;

        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++){
                cin>>a[i][j];
                dp[i][j]=max(dp[i-1][j]+a[i][j], dp[i][j-1]+a[i][j]);
            }
                
        cout<<dp[n][m]<<endl;
    }
}

int main(){
    work();
    return 0;
}

4.2 最低通行费

// http://ybt.ssoier.cn:8088/problem_show.php?pid=1287

/**
 * 花费时间不超过2n-1说明不能走回头路， 所以类似于摘花生
 * 但值得注意的是，
 * 摘花生求的是最大和，所以可以把0行和0列上的a值看做0；
 * 这里是求最小和，所以还是要特判
*/

#include<bits/stdc++.h>
using namespace std;

const int N = 110, INF=0x3f3f3f3f;

int a[N][N];
int dp[N][N];

int n, m;

void work(){
    cin>>n;
    m=n;

    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            cin>>a[i][j];
            if(i==1&j==1) dp[i][j]=a[i][j];
            else{
                dp[i][j]=INF;
                if(i-1>=1) dp[i][j]=min(dp[i][j], dp[i-1][j]+a[i][j]);
                if(j-1>=1) dp[i][j]=min(dp[i][j], dp[i][j-1]+a[i][j]);
            }
        }
            
    cout<<dp[n][m]<<endl;
}

int main(){
    work();
    return 0;
}

4.3 方格取数

// http://ybt.ssoier.cn:8088/problem_show.php?pid=1277

/**
 * 题意：从左上走到右下，走两次，但是同一个格子中的数只能取一次
 * 初步dp设想：dp[i1][j1][i2][j2]表示从分别从(1, 1) (1, 1)走到(i1, j1) (i2, j2)的和
 * 重要性质：考虑到每次每步只能走一格，而且终点坐标一样都是(n, n)，所以两次每步走过的格子满足i1+j1==i2+j2
 * 令i1+j1=i2+j2=k
 * 压缩状态：dp[k][i1][i2]
 * 
 * 集合划分：
 * i1-1 j1   i2-1 j2   -> k-1 i1-1 i2-1
 * i1   j1-1 i2   j2-1 -> k-1 i1   i2
 * i1-1 j1   i2   j2-1 -> k-1 i1-1 i2
 * i1   j1-1 i2-1 j2   -> k-1 i1   i2-1
 * 
 * 然后考虑加上两次的当前格
 * 如果i1==i2说明重合，只加一格的值
 * 否则分别加上(i1, k-i1) (i2, k-i2)的值
*/

#include<bits/stdc++.h>
using namespace std;

const int N=15;

int w[N][N];
int dp[2*N][N][N];

int n;

void work(){
    cin>>n;
    int a, b, c;
    while(cin>>a>>b>>c, a||b||c) w[a][b]=c;

    for(int k=2;k<=2*n;k++)
        for(int i1=1;i1<=n;i1++)
            for(int i2=1;i2<=n;i2++){
                int j1=k-i1, j2=k-i2;
                //判断坐标合法
                if(j1>=1&&j1<=n&&j2>=1&&j2<=n){
                    int t=w[i1][k-i1];
                    if(i2!=i1) t+=w[i2][k-i2];
                    int &x=dp[k][i1][i2];
                    x=max(x, dp[k-1][i1][i2]+t);
                    x=max(x, dp[k-1][i1-1][i2]+t);
                    x=max(x, dp[k-1][i1][i2-1]+t);
                    x=max(x, dp[k-1][i1-1][i2-1]+t);
                }
            }

    cout<<dp[2*n][n][n]<<endl;

}

int main(){
    work();
    return 0;
}