2025-02-15线段树（区间修改）

线段树（区间修改）

主要内容

区间修改与懒标记

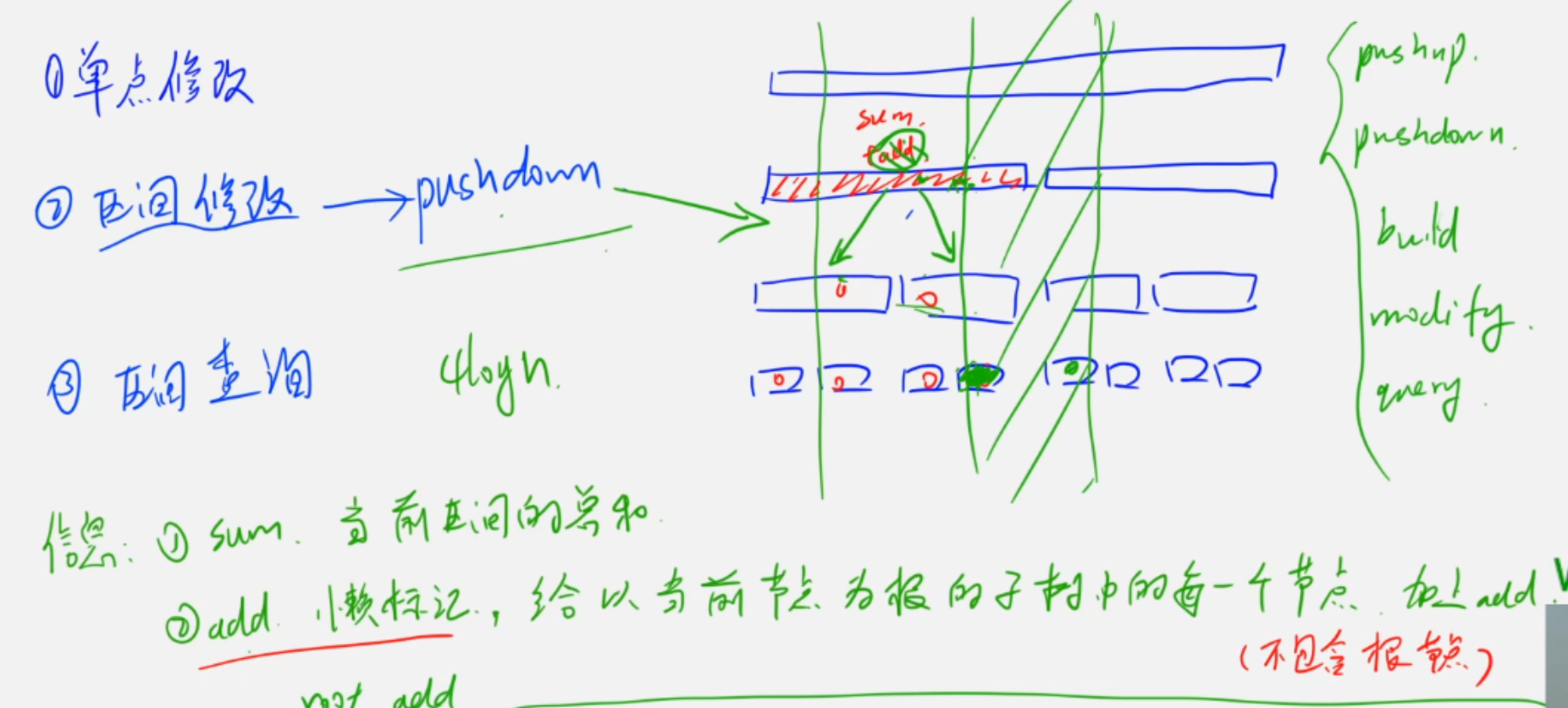
线段树是一种高效的数据结构，用于处理区间查询和修改操作。当涉及到区间修改时，懒标记（Lazy Propagation）是一种重要的优化手段，可以避免每次修改都直接更新所有节点，从而提高效率。懒标记的基本思想是将修改操作延迟到必要时才进行。

以下是懒标记的实现要点：

1. 标记存储：在每个节点中存储懒标记，表示当前节点的区间需要进行的修改操作。
2. 标记下推：在访问子节点之前，将当前节点的懒标记下推到子节点。
3. 标记清除：在将懒标记下推后，清除当前节点的懒标记。
4. 标记累积：如果当前节点已经有懒标记，新的修改操作需要与旧的懒标记进行累积。

扫描线算法

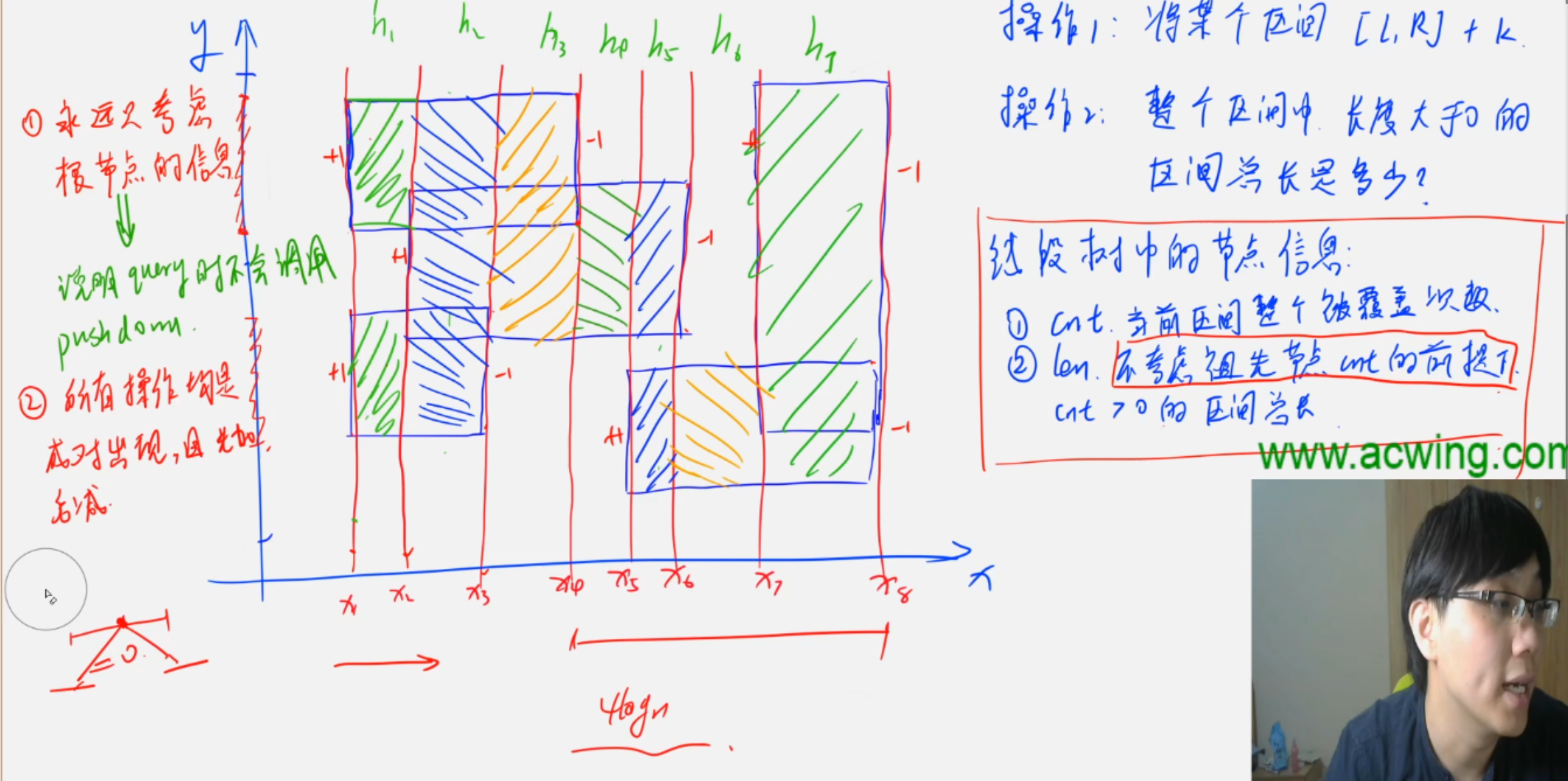
扫描线算法是一种用于处理几何问题（如矩形面积并、线段覆盖等）的算法。其基本思想是将问题分解为一系列事件（如线段的起点和终点），并按照某种顺序（通常是横坐标）处理这些事件。

以下是扫描线算法的实现要点：

1. 事件排序：将所有事件按照横坐标排序。
2. 线段树维护：使用线段树维护当前扫描线的覆盖状态。
3. 离散化：对于浮点数坐标，需要进行离散化处理。
4. 动态更新：在扫描过程中，动态更新线段树的状态，并计算结果。

注意：

1. 扫描线 算法解决覆盖区间求并的问题
2. 以x轴作为扫描的方向（要将线段按x大小排序），我们要计算的是扫过的面积，所以不包含第一条线
3. 线段树的端点是y方向上的区间（因为要维护长度!）， 映射tr[i].l ... tr[i].r对应ys[tr[i].l-1] ... ys[tr[i].r-1+1]
4. 由于y值可能为浮点数，所以需要离散化
5. 要维护的属性有cnt，入边+1， 出边-1；还有len，保存的是区间内的覆盖长度
6. 这里虽然要对区间进行修改，但是我们每次查询只针对根节点，即tr[1]，所以只要在modify及时pushup，就不需要pushdown操作
7. 扫描线虽然用到了线段树，但比较反常，所以背过是最好的方式-_-||

多个懒标记的累积

当线段树中存在多个懒标记时，需要正确处理它们的累积。例如，在区间加法和乘法的组合操作中，需要先处理乘法标记，再处理加法标记。累积公式如下：

• 乘法标记累积：mul_new = mul * mul'
• 加法标记累积：add_new = add * mul' + add'

例题

一个简单的整数问题2

// https://www.luogu.com.cn/problem/U250323

/* 经典区间修改，单点查询，需要懒标记*/

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

const int N=1e5+10;

struct Node{
    int l, r;
    ll sum;
    int add;
}tr[4*N];

int a[N];

void pushup(int u){
    tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
}

void pushdown(int u){
    /**
     * 向所有的子树进行 传播，但不修改 自己
    */
    auto &root=tr[u], &left=tr[u<<1], &right=tr[u<<1|1];

    if(root.add){
        left.add+=root.add, left.sum+=(ll)(left.r-left.l+1)*root.add;//注意左右子树可能已经被标记，需要累加
        right.add+=root.add, right.sum+=(ll)(right.r-right.l+1)*root.add;
        root.add=0;//消除懒标记
    }
}

void build(int u, int l, int r){
    tr[u]={l, r};

    if(l==r){
        tr[u].sum=a[l];
        return;
    } 

    int mid=l+r>>1;
    build(u<<1, l, mid), build(u<<1|1, mid+1, r);
    pushup(u);
}

void modify(int u, int l, int r, int add){
    if(tr[u].l>=l&&tr[u].r<=r){
        tr[u].sum+=(ll)(tr[u].r-tr[u].l+1)*add;
        tr[u].add+=add;//懒标记， 同样是要累加，不能直接赋值=
        return ;
    }

    pushdown(u);

    int mid=tr[u].l+tr[u].r>>1;
    if(l<=mid) modify(u<<1, l, r, add);
    if(r>mid) modify(u<<1|1, l, r, add);

    pushup(u);
}

ll query(int u, int l, int r){

    if(tr[u].l>=l&&tr[u].r<=r) return tr[u].sum;

    pushdown(u);

    ll res=0;
    int mid=tr[u].l+tr[u].r>>1;
    if(l<=mid) res+=query(u<<1, l, r);
    if(r>mid) res+=query(u<<1|1, l ,r);

    return res;
}

int n, m;

void work(){
    scanf("%d%d", &n, &m);

    for(int i=1;i<=n;i++) scanf("%d", &a[i]);

    build(1, 1, n);

    while(m--){
        char op[2];

        scanf("%s", op);

        if(*op=='C'){
            int l, r, d;
            scanf("%d%d%d", &l, &r, &d);

            modify(1, l, r, d);
        }else{
            int l ,r;
            scanf("%d%d", &l, &r);

            printf("%lld\n", query(1, l, r));
        }
    }
}

int main(){
    work();
    return 0;
}

亚特兰蒂斯

// https://www.acwing.com/problem/content/249/

/**
 * 1. 扫描线 算法解决覆盖区间求并的问题
 * 2. 以x轴作为扫描的方向（要将线段按x大小排序），我们要计算的是扫过的面积，所以不包含第一条线 
 * 3. 线段树的端点是y方向上的区间（因为要维护长度!）， 映射tr[i].l ... tr[i].r对应ys[tr[i].l-1] ... ys[tr[i].r-1+1]
 * 
 *        1    2   3   4   ...   
 *           1   2   3  ...        
 * 4. 由于y值可能为浮点数，所以需要离散化
 * 5. 要维护的属性有cnt，入边+1， 出边-1；还有len，保存的是区间内的覆盖长度
 * 6. 这里虽然要对区间进行修改，但是我们每次查询只针对根节点，即tr[1]，所以只要在modify及时pushup就可以，不需要pushdown操作
 * 
 * 总结：扫描线虽然用到了线段树，但比较反常，所以背过是最好的方式-_-||
*/

//review
#include<bits/stdc++.h>
using namespace std;

const int N=10010;

struct Segment{
    double x, y1, y2;
    int k;//入边+1，出边-1
    bool operator<(const Segment& t)const{
        return x<t.x;
    }
}seg[2*N];//一个矩形有两条扫描线

vector<double> ys;//离散化y坐标

int find(double x){
    int l=0, r=ys.size()-1;
    while(l<r){
        int mid=l+r>>1;
        if(ys[mid]>=x) r=mid;//[l, mid]
        else l=mid+1;
    }
    return l+1; // 下标从1开始
}

struct Node{
    int l, r;
    int cnt;
    double len;
}tr[2*N*4];

void pushup(int u){
    if(tr[u].cnt) tr[u].len=ys[(tr[u].r-1)+1]-ys[tr[u].l-1];
    else if(tr[u].l!=tr[u].r) tr[u].len=tr[u<<1].len+tr[u<<1|1].len;
    else tr[u].len=0;
}

void build(int u, int l, int r){
    tr[u]={l, r, 0, 0};
    if(l!=r){
        int mid=l+r>>1;
        build(u<<1, l, mid), build(u<<1|1, mid+1, r);
        //pushup(u);
    }
}

void modify(int u, int l, int r, int d){
    if(tr[u].l>=l&&tr[u].r<=r) {
        tr[u].cnt+=d;
        pushup(u);//要及时pushup，因为没有用专门的函数去执行query操作
        return ;
    }

    int mid=tr[u].l+tr[u].r>>1;
    if(l<=mid) modify(u<<1, l, r, d);
    if(r>mid) modify(u<<1|1, l, r, d);

    pushup(u);
}

int n;

void work(){
    int t=1;
    while(scanf("%d", &n), n){//n=0退出
        //多条测试样例时，每次都要记得初始化操作！！！
        ys.clear();//清空ys

        printf("Test case #%d\n", t++);

        int idx=0;
        for(int i=0;i<n;i++){
            double x1, y1, x2, y2;
            scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);

            ys.push_back(y1), ys.push_back(y2);

            seg[idx++]={x1, y1, y2, 1}, seg[idx++]={x2, y1, y2, -1};
        }

        sort(ys.begin(), ys.end());
        ys.erase(unique(ys.begin(), ys.end()), ys.end());

        sort(seg, seg+2*n);

        build(1, 1, ys.size()-1);//m个端点，m-1条线段

        double res=0;
        for(int i=0;i<2*n;i++){
            if(i!=0) res+=tr[1].len*(seg[i].x-seg[i-1].x);//起点线不需要
            modify(1, find(seg[i].y1), find(seg[i].y2)-1, seg[i].k);
        }

        printf("Total explored area: %.2lf\n\n", res);
    }
}

int main(){
    work();
    return 0;
}

维护序列

// http://ybt.ssoier.cn:8088/problem_show.php?pid=1551

/**
 * 修改区间的方式有两种，所以我们需要考虑顺序问题，先乘后加可以维持懒标记的格式
 * (sum * mul + add) * mul' + add' = sum * mul * mul' + add * mul' + add'
 * 得到累积懒标记:
 * mul_new = mul * mul'
 * add_new = add * mul' + add' 
*/

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

int n, p, m;
const int N=1e5+10;

struct Node{
    int l, r;
    ll sum;

    ll add, mul;

    Node(){add=0, mul=1;}
}tr[4*N];

int a[N];

void pushup(int u){
    tr[u].sum=(tr[u<<1].sum+tr[u<<1|1].sum)%p;
}

void lazy(Node& t, ll add, ll mul){
    t.sum=(t.sum*mul+add*(t.r-t.l+1))%p;//只应用当前的修改

    //累积修改
    t.mul=(t.mul*mul)%p; 
    t.add=(t.add*mul+add)%p; 
}

void pushdown(int u){
    auto &root=tr[u], &left=tr[u<<1], &right=tr[u<<1|1];
    int mul=root.mul, add=root.add;

    if(!(root.add==0&&root.mul==1)){
        lazy(left, add, mul);
        lazy(right, add, mul);
        root.add=0, root.mul=1;
    }
}

void build(int u, int l, int r){
    tr[u].l=l, tr[u].r=r;
    
    if(l==r){
        tr[u].sum=a[l];
        return;
    }

    int mid=l+r>>1;
    build(u<<1, l, mid), build(u<<1|1, mid+1, r);

    pushup(u);
}

void modify(int u, int l, int r, int add, int mul){
    if(tr[u].l>=l&&tr[u].r<=r){
        lazy(tr[u], add, mul);
        return ;
    }

    pushdown(u);

    int mid=tr[u].l+tr[u].r>>1;
    if(l<=mid) modify(u<<1, l, r, add, mul);
    if(r>mid) modify(u<<1|1, l, r, add, mul);

    pushup(u);
}

ll query(int u, int l, int r){
    if(tr[u].l>=l&&tr[u].r<=r) return tr[u].sum%p;

    pushdown(u);

    int mid=tr[u].l+tr[u].r>>1;
    ll res=0;
    if(l<=mid) res+=query(u<<1, l, r);
    if(r>mid) res+=query(u<<1|1, l, r);

    return res%p;
}


void work(){
    scanf("%d%d", &n, &p);

    for(int i=1;i<=n;i++) scanf("%d", &a[i]);

    build(1, 1, n);

    scanf("%d", &m);

    while(m--){
        int op, l, r;
        scanf("%d%d%d", &op, &l, &r);

        if(op==1){
            int c;
            scanf("%d", &c);
            modify(1, l, r, 0, c);
        }else if(op==2){
            int c;
            scanf("%d", &c);
            modify(1, l, r, c, 1);
        }else{
            printf("%lld\n", query(1, l, r));
        }  
    }
}

int main(){
    work();
    return 0;
}